Autonomous Drone Racing with Deep Reinforcement Learning
Deep Reinforcement Learning을 활용한 자율 드론 레이싱
이 글은 Song et al.의 Autonomous Drone Racing with Deep Reinforcement Learning을 요약한 것이다.
논문은 deep reinforcement learning을 이용해 드론의 준최적 시간 궤적을 생성하는 방법을 제안한다.
배경
자율 드론 레이싱은 복잡한 3차원 공간에서 최단 시간 내에 여러 게이트를 통과해야 하는 도전적인 과제다. 이는 시간 최적화(time-optimal) 문제로, AlphaPilot, Game of Drones 등의 대회에서 다뤄졌다. 이 대회들은 인간 전문 파일럿보다 뛰어난 성능을 달성하는 것을 목표로 하고 있다.
기존의 접근 방식들은 각각 장단점을 가지고 있었다. 최적화 기반 방법은 정확한 최적해를 도출할 수 있지만, 계산 시간이 매우 길어 실시간 적용이 어렵다는 단점이 있다. 반면, 다항식 궤적 생성 방식은 빠른 계산이 가능하지만 드론의 실제 동역학을 충분히 반영하지 못하는 한계가 있다. 샘플링 기반 방법 역시 빠른 계산이 가능하지만, 드론의 전체 상태 공간을 고려하지 못하는 문제가 있다.
| 방법 | 계산 복잡도 | 장점 | 단점 |
|---|---|---|---|
| 최적화 기반 | O(N^3) | 정확한 최적해 도출 | 계산 시간이 매우 길다 |
| 다항식 궤적 생성 | O(1) | 빠른 계산 | 드론 동역학 반영 부족 |
| 샘플링 기반 | O(1) | 빠른 계산 | 전체 상태 공간 고려 못함 |
이러한 기존 방법들의 한계를 극복하기 위해, 본 논문에서는 deep reinforcement learning을 활용한 새로운 접근 방식을 제안한다.
접근법
논문에서는 이 문제를 마르코프 결정 과정(Markov Decision Process, MDP)으로 정의하였다. 이 접근법은 드론의 현재 상태와 환경 정보를 바탕으로 최적의 행동을 결정하는 과정을 모델링한다.
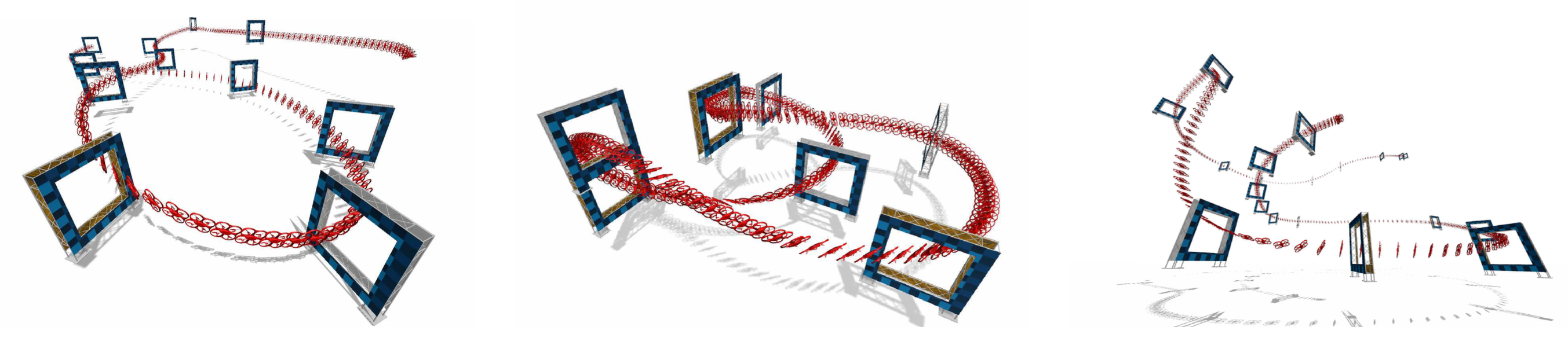세 가지 다른 레이스 트랙에서 고속으로 주행하는 쿼드로터 궤적. AlphaPilot (왼쪽), Split-S (중앙), AirSim (오른쪽)
State는 드론의 현재 상태와 게이트의 관측값으로 구성된다. 드론의 상태에는 위치, 속도, 자세, 각속도 등이 포함되며, 게이트 관측값은 드론을 기준으로 한 상대적 위치와 방향 정보를 포함한다. 이러한 상태 정보를 바탕으로 정책은 각 로터의 추력을 결정하는 action을 출력한다.
드론의 성능을 평가하는 보상 함수는 다음과 같이 정의된다:
$r(t) = r_p(t) + a \cdot r_s(t) - b \cdot \vert\vert\omega_t\vert\vert^2 + r_T$
여기서 $r_p(t)$는 경로 진행도 보상으로, 드론이 얼마나 효율적으로 경로를 따라가고 있는지를 평가한다. $r_s(t)$는 안전 보상으로, 드론이 게이트 중심을 정확히 통과하도록 유도한다. \vert\vert\omega_t\vert\vert^2항은 과도한 회전을 억제하기 위한 각속도 페널티이며, $r_T$는 게이트와의 충돌 시 적용되는 페널티이다.
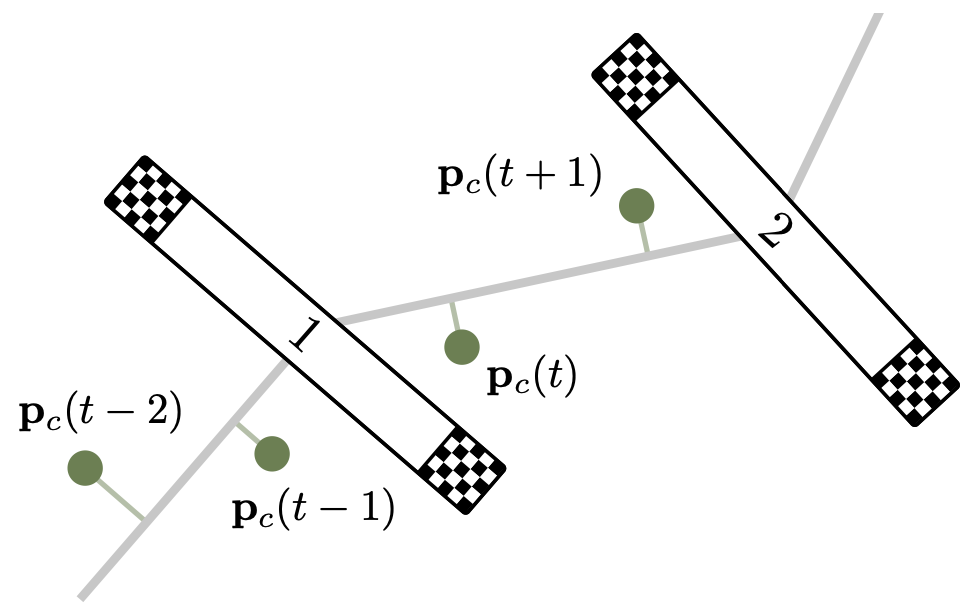경로 진행도 보상 계산 도식
경로 진행도 보상 $r_p(t)$는 다음과 같이 계산된다: $r_p(t) = s(p_c(t)) - s(p_c(t-1))$
여기서 $s(p) = \frac{(p - g_1)\cdot (g_2 - g_1)}{\vert\vert g_2 - g_1\vert\vert}$이며, $p_c$는 드론의 현재 위치, $g_1$과 $g_2$는 연속된 두 게이트의 중심 위치이다.
안전 보상 $r_s(t)$는 다음과 같이 정의된다: $r_s(t) = -f^2 \cdot (1 - \exp(-0.5 \cdot d_n^2 / v))$
여기서 $f = \max[1 - (d_p / d_{\max}), 0.0]$이고 $v = \max[(1 - f) \cdot (w_g / 6), 0.05]$이다. $d_p$와 $d_n$은 각각 드론과 게이트 평면 사이의 거리, 드론과 게이트 법선 사이의 거리를 나타낸다.
정책 학습 기법
학습을 위해 근사 정책 최적화(Proximal Policy Optimization, PPO) 알고리즘을 사용한다. 주요 특징은 다음과 같다:
- 상대적 게이트 관측값(Relative Gate Observations)을 입력으로 사용
- 병렬화된 샘플링 기법(Parallelized Sampling Scheme) 활용
- 3차원 경로 진행도(Path Progress)를 보상으로 사용
드론의 동역학 모델(Dynamics Model)은 다음과 같이 표현된다:
$\dot{p}_{WB} = v{WB}$
$\dot{q}{WB} = \frac{1}{2}\Lambda(\omega_B) \cdot q{WB}$
$\dot{v}{WB} = q{WB} \bigodot c + g$
$\dot{\omega}_B = J^{-1}(\eta - \omega_B \times J\omega_B)$
여기서 $p_{WB}$, $v_{WB}$는 위치와 속도, $q_{WB}$는 쿼터니언 방향(Quaternion Orientation), $\omega_B$는 각속도(Angular Velocity)를 나타낸다.
관측 및 행동 공간은 다음과 같이 생성된다:
- 관측(Observation): $s_t^{\text{track}} = [o_1, \alpha_1, …, o_i, \alpha_i, …]$, $i \in [1, …, N]$
- $o_i$: i번째 게이트의 구면 좌표계 관측값 $(p_r, p_\theta, p_\phi)$
- $\alpha_i$: 게이트 법선과 드론-게이트 중심 벡터 사이의 각도
- 행동(Action): $a_t = [f_1, f_2, f_3, f_4]$ (개별 로터 추력 명령)
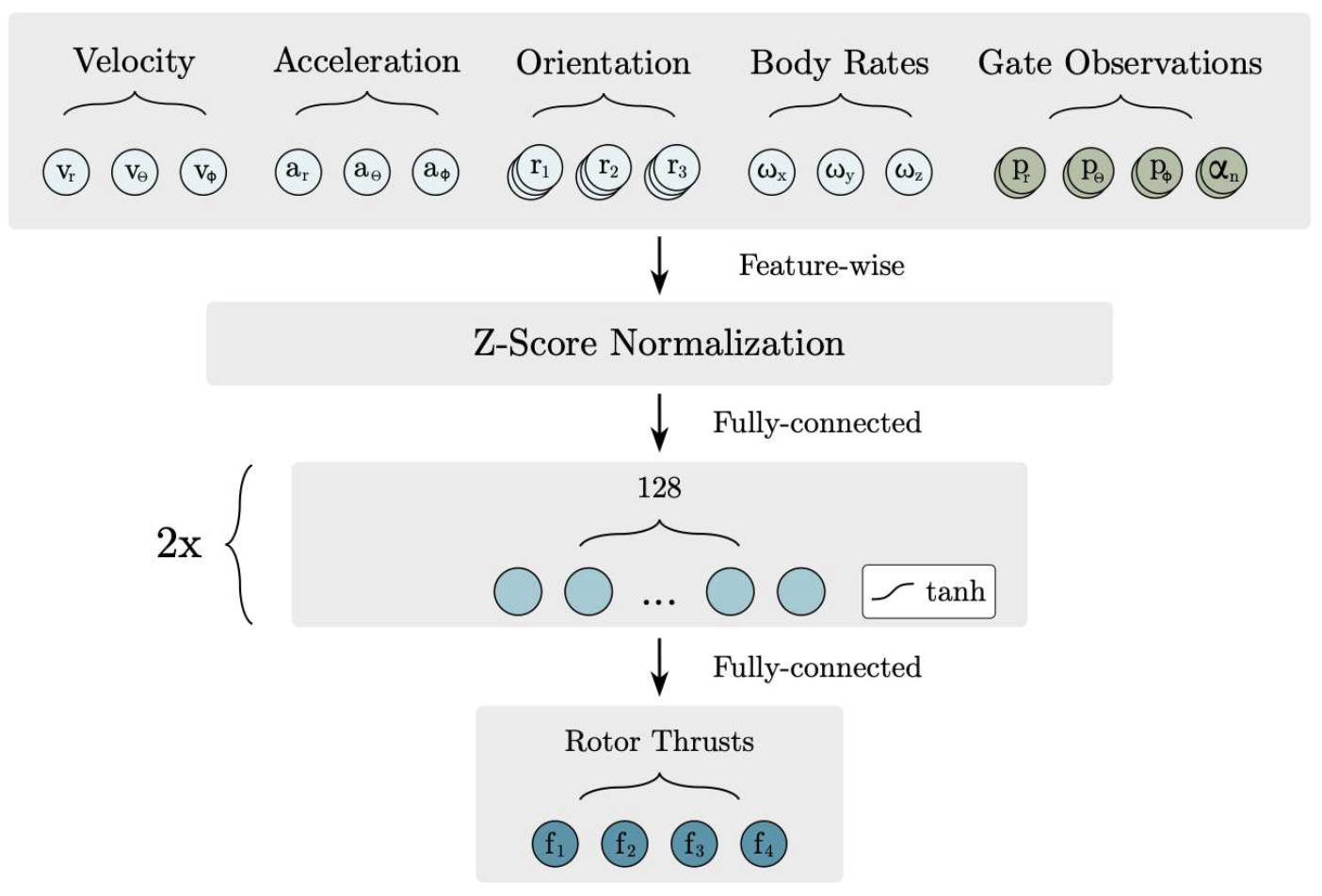관측 벡터와 네트워크 아키텍처
학습 과정의 효율성을 높이기 위해 몇 가지 기법들이 도입되었다. 먼저, 병렬 샘플링 기법을 통해 최대 100개의 환경에서 동시에 데이터를 수집한다. 이는 학습 속도를 향상시키고, 다양한 상황에 대한 경험을 빠르게 축적할 수 있게 해준다.
또한, 분산 초기화 전략을 통해 드론이 트랙의 다양한 부분에서 학습을 시작할 수 있도록 한다. 초기에는 모든 경로 세그먼트 주변에서 호버 상태로 초기화하고, 학습이 진행됨에 따라 이전 궤적에서 샘플링한 상태로 초기화하는 방식을 사용한다. 이를 통해 전체 트랙에 대한 균형 잡힌 학습이 가능하다.
마지막으로, 랜덤 트랙 커리큘럼을 도입하여 정책의 일반화 성능을 향상시킨다. 학습 초기에는 비교적 단순한 트랙에서 시작하여 점진적으로 복잡한 트랙으로 난이도를 높여간다. 이러한 접근은 정책이 다양한 트랙 레이아웃에 적응할 수 있도록 한다. 랜덤 트랙 커리큘럼에서 트랙 생성기는 다음과 같이 정의된다:
$T = [G_1, …, G_{j+1}]$, $j \in [1, +\infty)$
여기서 $G_{j+1} = f(G_j, \Delta p, \Delta R)$로, 상대적 위치와 방향으로 게이트를 정의한다.
실험 결과
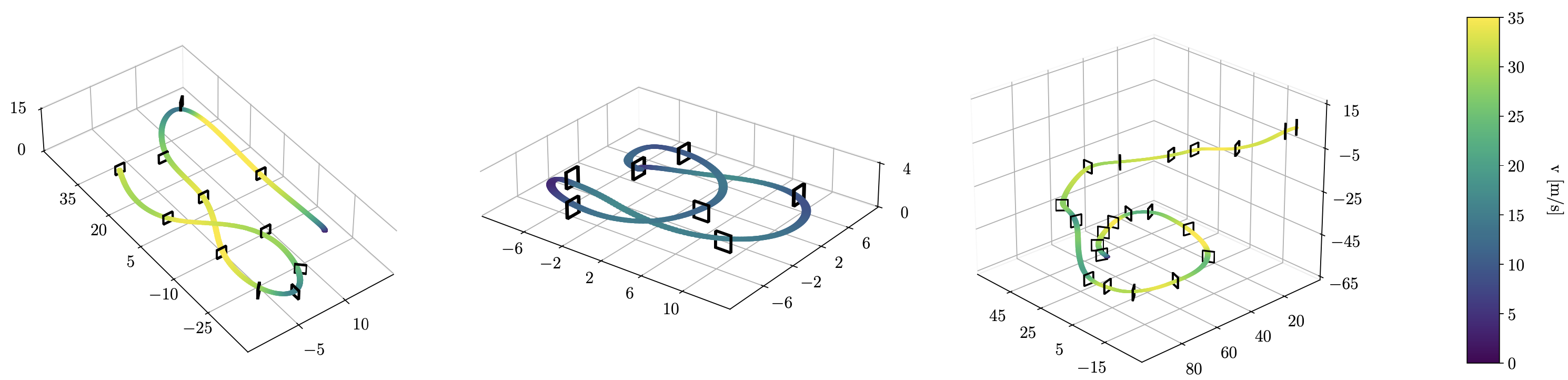레이스 트랙과 제안 기법으로 생성한 궤적. 좌에서 우로 AlphaPilot track, Split-S track, AirSim track
AlphaPilot, Split-S, AirSim의 세 가지 결정론적 트랙에서의 성능은 다음과 같이 비교된다:
| 트랙 | 다항식 방법 (s) | 최적화 방법 (s) | 제안 방법 (s) |
|---|---|---|---|
| AlphaPilot | 12.23 | 8.06 | 8.14 |
| Split-S | 15.13 | 6.18 | 6.50 |
| AirSim | 23.82 | 11.40 | 11.82 |
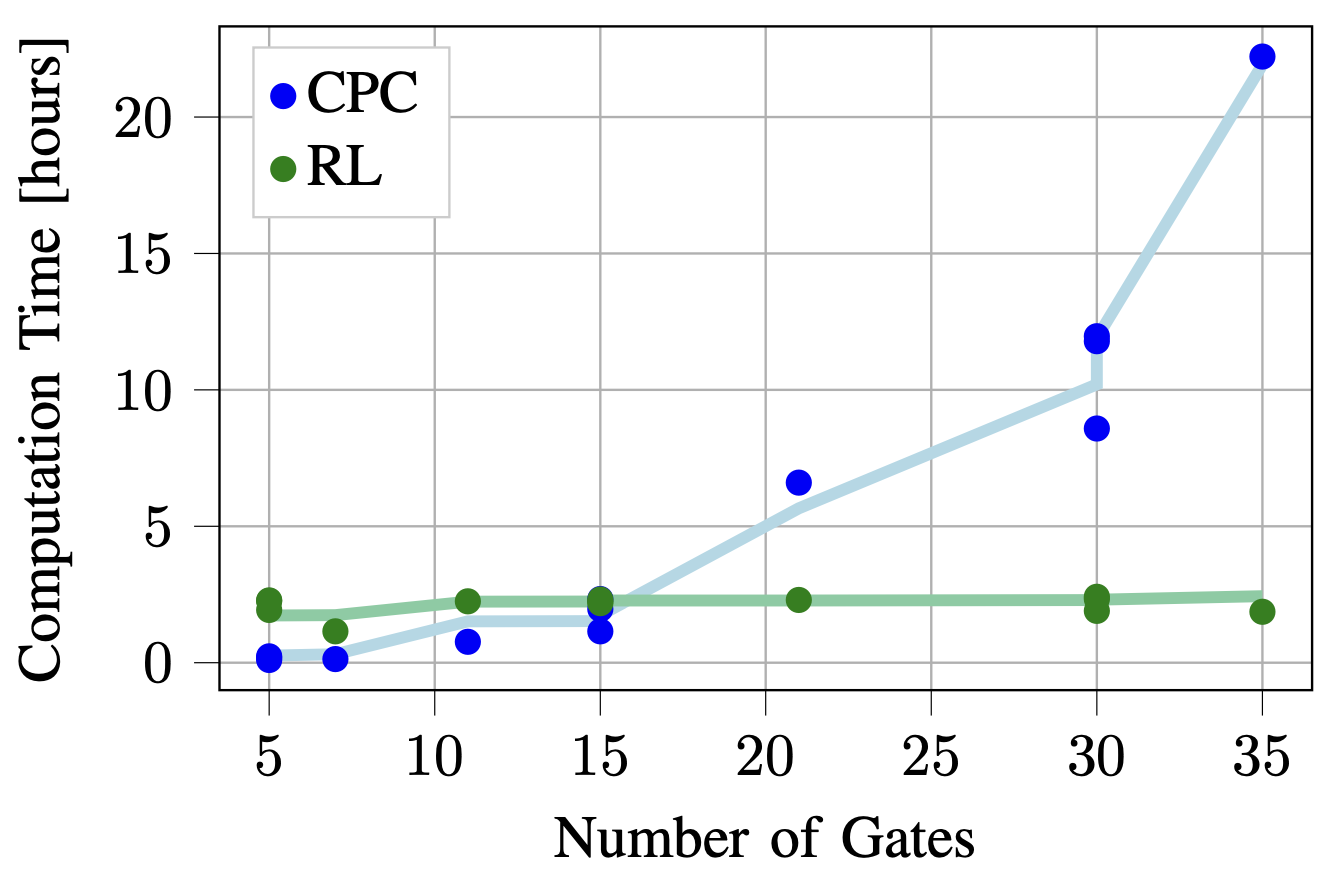제안 기법과 최적화 기법의 계산 시간 비교
결과를 보면 제안된 방법이 최적화 기반 방법에 근접한 성능을 보이면서도 다항식 방법보다는 우수한 성능을 달성했음을 알 수 있다.
트랙 변화에 대한 대응 능력을 평가하기 위해 AlphaPilot 트랙의 게이트 위치와 방향을 무작위로 변경하는 실험이 수행되었다. 97.5%의 성공률을 달성했으며, 결정론적 트랙 대비 랩타임이 단 2.21% 증가하는데 그쳤다. 이 결과는 제안 방법의 robustness를 보여준다.
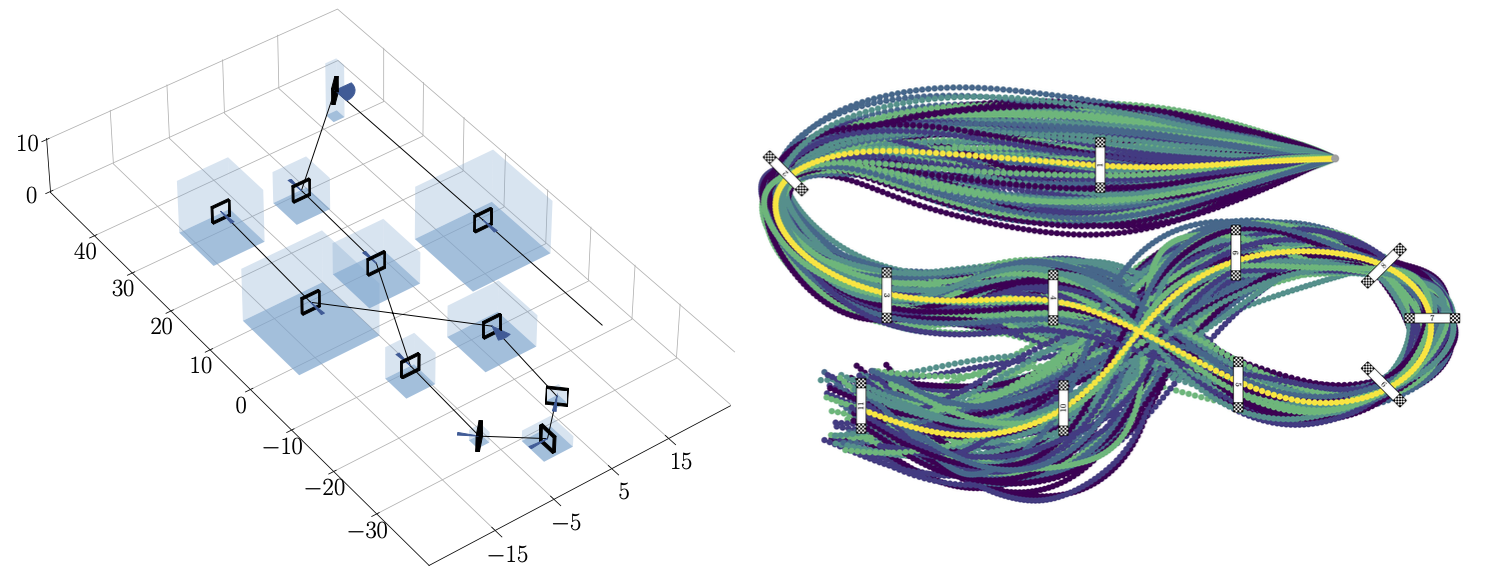트랙 변화에 따른 제안 기법의 robustness. 좌: 변경된 AlphaPilot track. 우: AlphaPilot track 구성 변화에 따른 궤적
트랙 변화 대응 능력 실험에서 게이트 무작위화 수준에 따른 성능은 다음과 같다:
| 게이트 무작위화 수준 | 평균 시간 (s) | 충돌 횟수 |
|---|---|---|
| 0.00 | 8.32 | 0 |
| 0.50 | 8.43 | 0 |
| 0.75 | 8.55 | 2 |
| 1.00 | 8.73 | 25 |
일반화 능력을 평가하기 위해 새로운 랜덤 트랙에서의 성능도 테스트하였다. 110m에서 150m 길이, 최대 17m의 고도 변화를 가진 랜덤 트랙에서 97.4%의 성공률을 기록했다. 이는 제안된 방법이 다양한 트랙 레이아웃에 잘 적응할 수 있음을 보여준다.
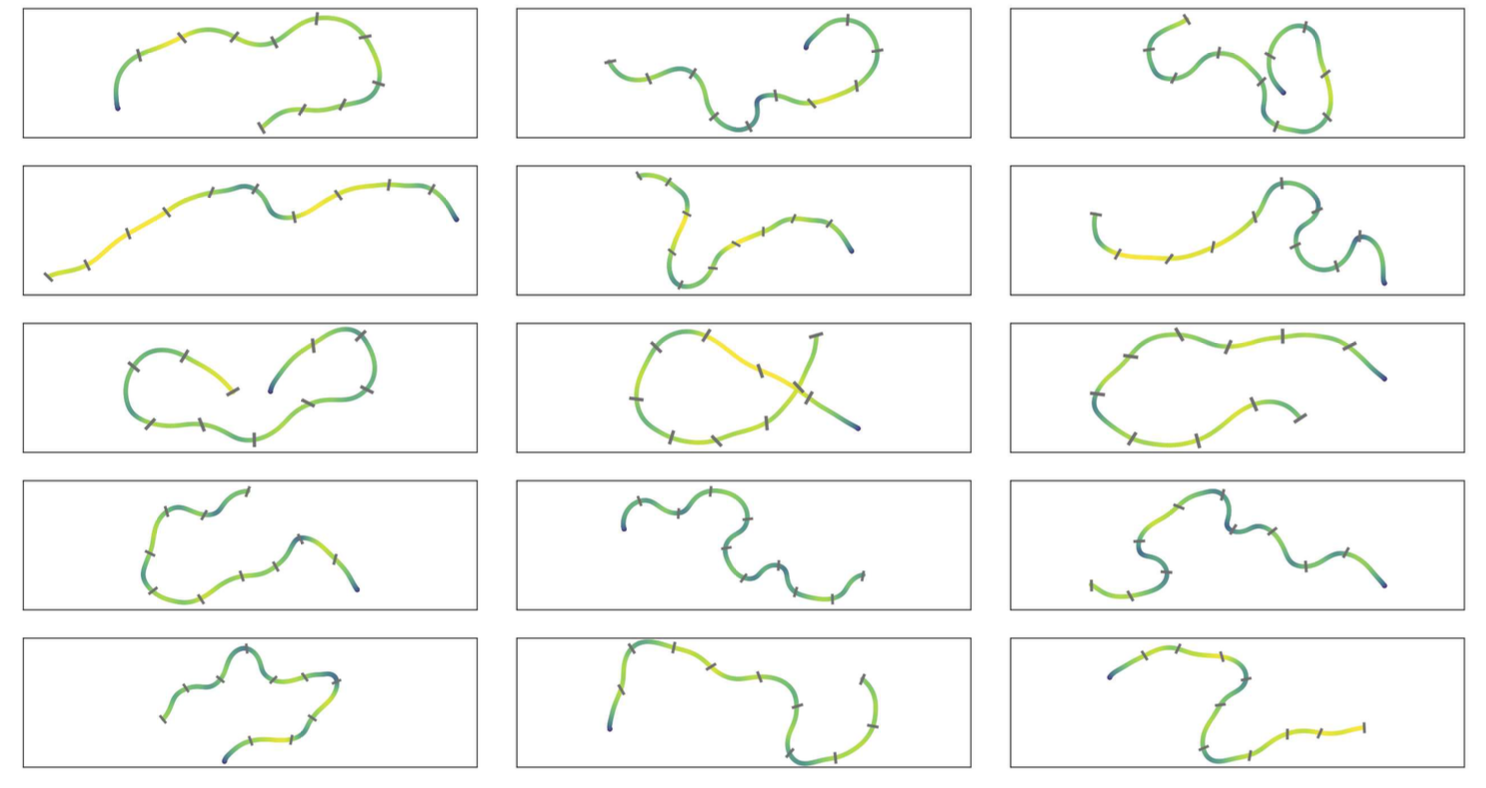랜덤 트랙에서 제안 기법으로 생성한 비행 경로 시각화
일반화 능력 평가를 위한 랜덤 트랙 실험에서는 안전 보상과 트랙 적응 전략의 효과를 다음과 같이 비교하였다:
| 안전 보상 | 트랙 적응 | 충돌 횟수 (1000번 시도 중) |
|---|---|---|
| X | X | 71 |
| X | O | 47 |
| O | O | 26 |
실제 드론을 이용한 테스트에서는 최대 60km/h의 고속 비행을 성공적으로 수행했다. 40m 길이의 실제 트랙에서 안정적인 비행을 보임으로써, 시뮬레이션에서 학습된 정책이 실제 환경에도 잘 전이될 수 있음을 확인한다.
실제 드론으로 학습된 경로를 추종 비행하는 장면
결론
이 연구는 deep reinforcement learning이 자율 드론 레이싱에서 준최적 궤적을 생성하는 데 효과적임을 보여준다. 특히 트랙 변화에 대한 적응력, 그리고 게이트 수에 독립적인 계산 효율성은 이 접근 방식의 장점이다.
그러나 아직 개선의 여지가 있는 부분들도 있다. 실제 환경에서의 궤적 추적 성능 향상, 더 복잡한 환경과 미션에 대한 적용, 다양한 드론 모델에 대한 일반화, 그리고 시뮬레이션과 실제 환경 간의 차이(sim-to-real gap)를 극복하는 것이 향후 연구 과제로 남아있다.